Noise in Communication Systems
The term noise refers to unwanted electrical signal in electrical systems. This unwanted signal masks the information signal, limiting the transmission rate and affecting the receivers ability to make the correct symbol decision.
In communication systems noise arises due to different sources, these sources can be classified in two categories:
- Natural noise:
- Atmospheric noise.
- Noise from the sun.
- Other galactic radiation sources.
- Man-made noise:
- Ignition noise.
- Radiating electromagnetic signals.
Engineers must try their best to eliminate noise, or at least reduce its affects. This can be achieved through filtering, shielding, good choice of modulation and optimal selection of receiver’s site, in remote dessert locations far from man-made noise sources.
Even with all these methods, there is one source of noise called Thermal noise, also known as Johnson noise that cannot be eliminated. Thermal noise occurs because of the thermal motion of electrons in different electronic components such as resistors and wires. The same electrons responsible for electronical conduction are responsible for making thermal noise.
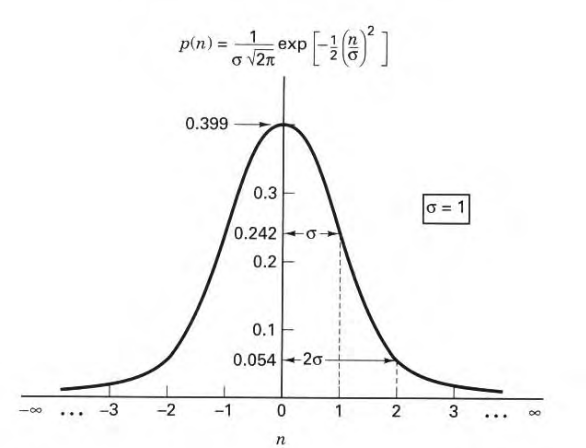
Thermal noise can be described as a zero-mean Gaussian random process. Statistically characterized by the Gaussian probability density function:
\[p(n)=\frac{1}{σ\sqrt{2\pi}}\exp[-\frac{1}{2}(\frac{n}{σ})^2]\]
Where \(σ^2\) is the variance of \(n\). We obtain the normalized Gaussian density function of a zero-mean process by assuming that \(σ = 1\). This normalized pdf function is shown in the figure below.
 |
|---|
| Normalized \(σ = 1\) Gaussian probability density function |
Random signals are often represented as the sum Gaussian noise random variable, and the dc component. The pdf \(p(z)\) function is written as:
\[p(z)=\frac{1}{σ\sqrt{2\pi}}\exp[-\frac{1}{2}(\frac{z-a}{σ})^2]\]
\[z = a + n\]
Where:
- \(z\) The random signal.
- \(a\) The dc component.
- \(n\) The Gaussian noise random variable.
White Noise
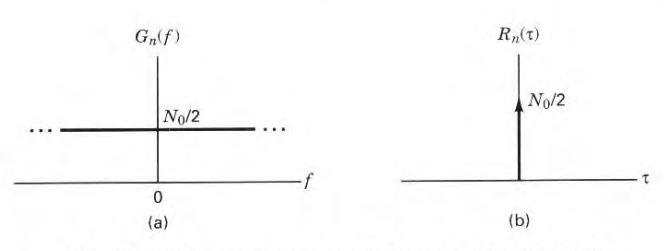
The power spectral density of the thermal noise is the same for all frequencies used in communication systems, that means it emanates an equal amount of noise power per unite bandwidth at all frequencies an from dc to \(10^{12} Hz\). The simplest model of thermal noise states that its power spectral density \(G_n(f)\) is flat for all these frequencies and equal to:
\[G_n(f) = \frac{N_0}{2} watts/hertz\]
The factor \(2\) indicates that the \(G_n(f)\) is a two-sided power spectral density. When the noise power has such a uniform spectral density it’s called a white noise. The autocorrelation function of white noise is given by the Inverse Fourier Transform of the \(G_n(f)\) function, as follows:
\[R_n(\tau)=\mathscr{F}^{-1}{G_n(f)} = \frac{N_0}{2} \delta(\tau)\]
Thus the autocorrelation of white noise is delta function weighted at \(\tau = 0\) and is zero for \(\tau\neq0\). So any two different samples of white noise are uncorrelated, from its time shifted version. since thermal noise is a Gaussian process and the samples are uncorrelated, the noise samples are also independent. Therefore the effect on the detection process of a channel with additive white Gaussian Noise (AWGN) is that the noise affects each transmitted signal independently. The term additive means that the noise is added to the signal. As the bandwidth of white noise is infinite, thus its average power is also infinite:
\[\int_{-\infty}^{\infty} \! \frac{N_0}{2} \, \mathrm{d}f = \infty\]
 |
|---|
| (a) Power spectral density of white noise |
| (b) Autocorrelation function of white noise |
In real life applications, no noise process can be truly white. however most noise processes in real life can be assumed to be approximately white.
SNR
The Signal to Noise Ratio ( SNR ) is defined as the ratio of the signal power ( information signal ) to the power of noise ( unwanted signal ):
\[SNR = \frac{P_{signal}}{P_{noise}}\]
\[SNR_{dB} =\log_{10}{ (\frac{P_{signal}}{P_{noise}})}\]
Conclusion
In this article we briefly talked about noise in communication systems, described thermal noise mathematically and showed that thermal noise can be approximately assumed to be white noise. Finally we introduced the term SNR and explained it briefly.
I hope you liked this article, please stay tuned for more.