Autocomplete

Autocomplete is the feature when an application predicts the complete word, after just typing some prefix of the word. You must have used autocomplete feature a lot in your life in many area like:

Search engines, Google search engine suggests to you an autocomplete feature when you type some text in the search bar, usually sorted by most trends.
Emails, as you start writing some prefix of the Email address you will get a list of suggestions.
Social media, like facebook, linkedin, instagram…
In source code editors, actually I am using Atom right now and I have used autocomplete for at least 10 times just in the first small part of this article.


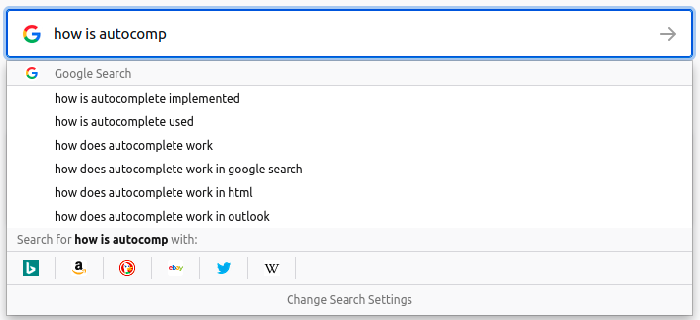Figure 1: Autocomplete with Google Search Engine

Autocomplete can be a powerful tool to minimize the number of keystrokes needed to type a word, also in some cases like search engines it helps you to get good suggestions about what you are looking for, however implementing autocomplete is not an easy task, you should know the right data structures to use to archive the best space and time complexity. In this article I will be talking about two different implementations using Trie and Ternary Search Trees data structures.

Trie

Trie is a tree-like data structure used to store strings, it supports insert, search and delete operations in \(O(n)\) time. Each node of the trie contains an array of pointers for every character of the alphabet, in addition to a Boolean flag to indicate the end of string. The basic TrieNode implementation in C++ looks like:

const int ALPHABET_SIZE = 26;
struct TrieNode{
    bool end_of_string;
    TrieNode *pointer[ALPHABET_SIZE];
    TrieNode(){
        end_of_string = 0;
        for (int i=0;i<ALPHABET_SIZE;i++) pointer[i] = NULL;
    }
}*root = new TrieNode();

This is a trie that stores the list of strings: ["CAR", "CAT", "CODE", "CODER", "PAPER", "TREE", 'TRIE']. The first empty node is the root of the trie, nodes that are terminate words are marked with light green. In this figure I only showed the non null pointers, if I wanted to show the null pointers it will look a complete mess, now this thing makes Trie data structure inefficient in space complexity, I will be talking about that later on.


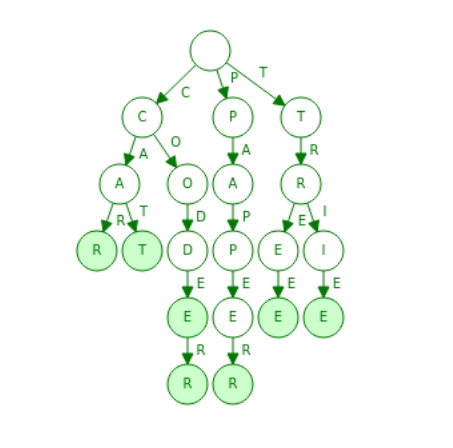Figure 2: Basic Trie structure

Insert string to Trie

To insert a string in the trie, every character of the input string is inserted as an individual TrieNode. The children of this node are pointers to the next TrieNodes. If the character in the input string is already existing in the pointers array we follow the pointer in the current TrieNode array of pointers, however if the character is null we need to construct it. When we reach the last character of the string we set the value of the end_of_string flag to be true.

The implementation of the insert function in C++ looks like:

void insert(string str){
    TrieNode *cur = this;
    int n = str.length();
    for(int i=0;i<n;i++){
        int nx = str[i]-'A';
        if(cur->pointer[nx]==NULL)cur->pointer[nx] = new TrieNode();
        cur = cur->pointer[nx];
        if(i==n-1)cur->end_of_string = true;
    }
}    

Search for string in the Trie

In search operation we also start from the root of the trie and check if every character in the string is existing, the search ends with failure if some character is not existing, or we reach the end of the string and the end_of_string flag is not set, otherwise the search is success. The implementation of the search function in C++ looks like:
```
bool search(string str){
  TrieNode *cur = this;
  int n = str.length();
  for(int i=0;i<n;i++){
      int nx = str[i]-'A';
      if(cur->pointer[nx]==NULL)return false;
      cur = cur->pointer[nx];
  }
  return cur->end_of_string;
}
```

Prefix autocomplete using Trie

The autocomplete function is an extension to the search function, first we search for the given prefix, then do a traversal of the tree starting from the end node of the search. Every time we reach a node with the end_of_string flag set, we add this string to the list of words. This traversal can be either bfs or dfs. The implementation of the autocomplete function in C++ looks like:

vector<string> AutoComplete(string str){
  TrieNode *cur = this;
  vector<string>ret;
  int n = str.length();
  for(int i=0;i<n;i++){
      int nx = str[i]-'A';
      if(cur->pointer[nx]==NULL)return ret;
      cur = cur->pointer[nx];
  }
  return cur->bfs(str);
}

And the bfs traversal will be:

vector<string> bfs(string str){
  vector<string>ret;
  queue<pair<TrieNode*, string> >q;
  TrieNode *cur = this;
  q.push({cur, str});
  while(!q.empty()){
      TrieNode *cur = q.front().first;
      string str = q.front().second;
      q.pop();
      if(cur->end_of_string==true){
          ret.push_back(str);
      }
      if(ret.size()==MX_SIZE)break;
      for(int i=0;i<ALPHABET_SIZE;i++){
          if(cur->pointer[i]!=NULL){
              q.push({cur->pointer[i], str+char(i+'A')});
          }
      }
  }
  return ret;
}

Advantages and disadvantages of using trie

Trie is easy to implement, fast as all the operations (insert, search, delete, autocomplete) run in \(O(n)\), where \(n\) is the length of the input string, but in terms of space complexity trie is not the best choice, every node of the trie stores an array of pointers with size equal to ALPHABET_SIZE and most of these pointers are null pointers. In case of using lower case and upper case English letters, digits, punctuation marks, international characters… This can be very big and memory consuming. You can use trie in case of medium size data with small ALPHABET_SIZE.

Ternary Search Trees

Ternary Search Trees, also know as TST is similar to Binary Search Trees, in BST every node has a value and two pointers to two subtrees, pointer for the left child having value less than the current node, and pointer for the right child having value greater than the current node, in addition to that TST has an extra pointer often called the middle pointer, pointing for the child having value equal to the current node, TST also contains end_of_string flag, just like a normal trie. The basic TSTNode implementation in C++ looks like:

struct TSTNode{
    bool end_of_string;
    TSTNode *left, *right, *middle;
    char value;
    TSTNode(){
        end_of_string = 0;
        left = NULL;
        right = NULL;
        middle = NULL;
    }
}*root;

This is a TST that stores the list of strings: ["CAR", "CAT", "CODE", "CODER", "PAPER", "TREE", 'TRIE', 'TST']. Nodes that are terminate words are marked with light green.


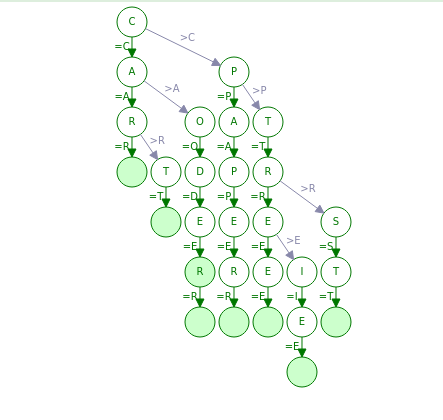Figure 3: Basic TST structure

Insert string to TST

Insertion to TST is an easy task, we jsut have to do character comparison between the string character and the current node character, if they are equal move to the middle child, if the string character is smaller then move to the left child, otherwise move to the right child, update the character value at every node, and check set the end_of_string flag in the last node, The implementation of the insert function in C++ looks like:

TSTNode *insert(TSTNode *head, string str, int idx){
  if(idx==str.length()){
      if(head==NULL)head = new TSTNode();
      head->end_of_string = true;
      return head;
  }
  if(head==NULL){
      head = new TSTNode();
      head->value = str[idx];
  }
  if(str[idx] == head->value)head->middle = insert(head->middle, str, idx+1);
  else if(str[idx] > head->value)head->right = insert(head->right, str, idx);
  else head->left = insert(head->left, str, idx);
  return head;
}

Search for string in the TST

Searching in the TST is similar to inserting, we start from the root of the TST and do character comparison at every node, and we go to the middle, left or right child, if we reach a null node then the string is not present in the TST, when we reach the last character of the string we need to check the value of the end_of_string flag, The implementation of the search function in C++ looks like:
```
bool search(string str){
  TSTNode *root = this;
  int n = str.length();
  int i = 0;
  while(i<n){
      if(root==NULL)return 0;
      if(root->value == str[i]){
          root = root->middle;
          i++;
          continue;
      }
      if(root->value < str[i])root = root->right;
      else root = root->left;
  }
  return root->end_of_string;
}
```
Prefix autocomplete using TST

Follows the same logic as using trie, the implementation of the search function in C++ looks like:

vector<string> bfs(string str){
    vector<string>ret;
    queue<pair<TSTNode*, pair<string, int> > >q;
    TSTNode *cur = this;
    q.push({cur, {str, 1}});
    while(!q.empty()){
        TSTNode *cur = q.front().first;
        string str = q.front().second.first;
        bool add = q.front().second.second;
        q.pop();
        if(cur->end_of_string==true && add==true){
            ret.push_back(str);
        }
        if(ret.size()==MX_SIZE)break;
        if(cur->left!=NULL)q.push({cur->left, {str, 0}});
        if(cur->middle!=NULL)q.push({cur->middle, {str + cur->value, 1}});
        if(cur->right!=NULL)q.push({cur->right, {str, 0}});
    }
    return ret;
}
vector<string> AutoComplete(string str){
    vector<string>ret;
    TSTNode *root = this;
    int n = str.length();
    int i = 0;
    while(i<n){
        if(root==NULL)return ret;
        if(root->value == str[i]){
            root = root->middle;
            i++;
            continue;
        }
        if(root->value < str[i])root = root->right;
        else root = root->left;
    }
    return root->bfs(str);
}

Advantages of using TST

TST is much more efficient in space complexity, also operations such as (insert, search, delete, autocomplete) run in \(O(n)\), where \(n\) is the length of the input string, TST can also be used as spell checker (I might consider writing an article about it). For the best performance of TST strings should be inserted randomly not in alphabetical order, if inserted in alphabetical order then each sub-tree that corresponds to a single trie node would degenerate into a linked list, significantly increasing the cost of searching.

Conclusion

In this article we started by talking about autocomplete feature, then we moved to trie data structure and explained the main functions of trie and how to use it in autocomplete, we then showed that trie is inefficient in terms of space complexity and then talked about Ternary Search Trees.

The full code for this problem is available here.

I hope you liked this article, please stay tuned for more.

Autocomplete

Trie

Insert string to Trie

Search for string in the Trie

Prefix autocomplete using Trie

Advantages and disadvantages of using trie

Ternary Search Trees

Insert string to TST

Search for string in the TST

Prefix autocomplete using TST

Advantages of using TST

Conclusion